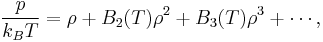Virial expansion

The classical virial expansion expresses the pressure of a many-particle system in equilibrium as a power series in the density. The virial expansion was introduced in 1901 by Heike Kamerlingh Onnes as a generalization of the ideal gas law. He wrote for a gas containing $N$ atoms or molecules,

$\frac{p}{k_BT} = \rho %2B B_2(T) \rho^2 %2BB_3(T) \rho^3%2B \cdots,$

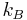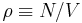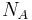where $p$ is the pressure, $k_B$ is the Boltzmann constant, $T$ is the absolute temperature, and $\rho \equiv N/V$ is the number density of the gas. Note that for a gas containing a fraction $n$ of $N_A$ (Avogadro's number) molecules, truncation of the virial expansion after the first term leads to 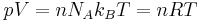$pV = n N_A k_B T = nRT$ , which is the ideal gas law.

Writing 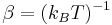$\beta=(k_{B}T)^{-1}$ , the virial expansion can be written in closed form as

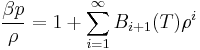$\frac{\beta p}{\rho}=1%2B\sum_{i=1}^{\infty}B_{i%2B1}(T)\rho^{i}$ .

The virial coefficients 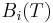$B_i(T)$ are characteristic of the interactions between the particles in the system and in general depend on the temperature $T$ .

Virial expansion

See also